並べなおすと１マス減る三角形のトリックを視覚的に解析

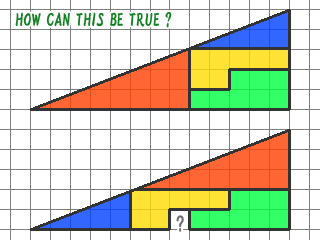
このような不思議な図形をご存知でしょうか？三角形を切り分け並べなおすと、同じ面積のはずなのに１マス少なくなってしまうというもの。そんなことあるはずないのだけど、確かに減っている！？

これにはトリックがあるに違いない。そこで、面積を計算するなどの難しい理屈は抜きにして、視覚的に分かりやすく「正確な並べなおし」で検証してみました。図形は3Dソフト(Softimage/XSI)を使用して正確に描画します。

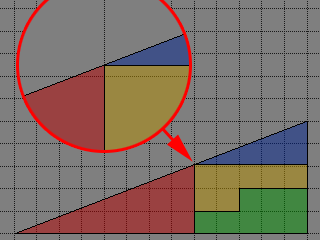
まず、正確にマス目に沿って三角形を切り分けます。直角の部分から左に５、上に３…あれ？おかしい。ここで切り分けると、斜め線はマス目の交点で切り分けられません。というか、横13・縦5の斜め線は、マス目の交点を通る箇所はできません。問題の絵では線を太くしてそれが分かり辛くなってます。ここは、横方向だけマス目に合わせて切り分けました。

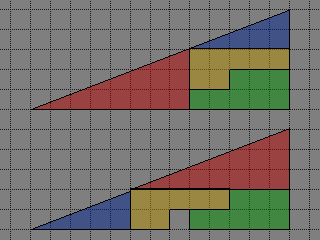
問題の絵のように並べなおします。おお、１マス減っている？しかし、よく見ると一部線が重なっているような…

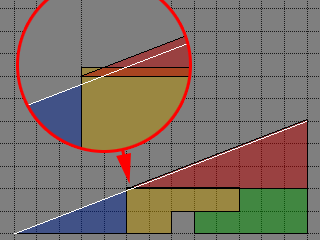
拡大してみると、重なっている部分とはみ出ている部分があります。問題の絵の線が太いのは、それをごまかしていたのです。

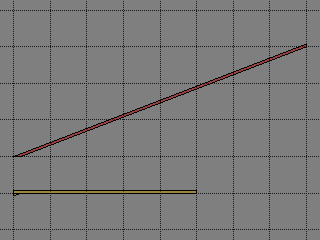
重なり・はみ出し部分を切り出してみました。きっと、この部分が消失した１マス分の原因ですよ。細いけど、合計すると１マス分あるに違いない。

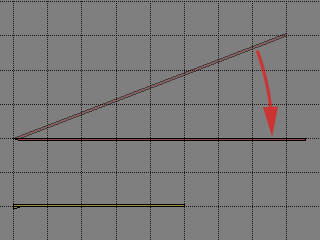
まず、斜め部分は切り取りやすいよう、真っ直ぐに回転する。

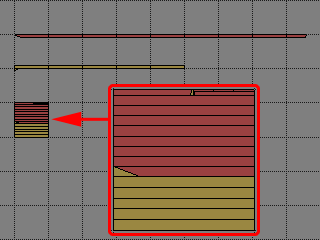
そして、正確に切り取って配置してみました。きっちり１マス分埋まった！

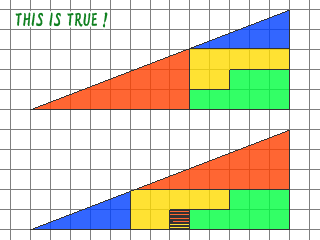
太い線に隠れていた部分を正確に描画すると、本当はこうなります。１マスは、なくなってはいませんでした。

→ 追記：三角形に見えて実は四角形

　

　

　

コメント(35)